Text Compression
After finishing my book, I began to carry out a practical application of the book's philosophy to the domain of text and language. The idea is to develop theories of syntax, incorporate them as text compression programs, and then evaluate them by looking at the compression rates they achieve on a large corpus.
This research can be understood in comparison to the related fields of mainstream linguistics and natural language processing (NLP). In comparison to linguistics, my research is much more quantitative and rigorous. The compression requirement demands the highest possible level of rigor. It is simply impossible to achieve lossless compression using a theory of syntax that is inadequately specified, internally inconsistent, or empirically inaccurate. My belief is that the level of rigor mandated by the compression philosophy will enable me to discover high-quality theories of syntax that will shed new light on long-standing questions, enable new applications in areas such as information retrieval or machine translation, and highlight interesting new issues for further study.
In comparison to NLP, my research is more curiousity-driven and empirically oriented. NLP is largely the application of machine learning methods to text databases. Most research in this area follows a fairly standard formula: define an application (say, sentiment analysis), obtain a labeled database, perform some preprocessing or feature selection to the text, and then apply a general purpose machine learning algorithm, such as a support vector machine. For the most part, NLP researchers do not have an intrinsic interest in the structure of text. Their basic philosophy is that a smart learning algorithm should obviate the need for linguistic knowledge. This stance is summed up by Fred Jelinek's comment that "Every time I fire a linguist, the performance of the speech recognizer goes up." In contrast, my view is that the algorithm is a tool that can enhance our understanding of lingustics. My research is entirely focused on the search for and description of empirical regularities in text (these regularities can be exploited by the compressor to achieve shorter codelengths). I am not primarily motivated by the goal of building practical applications, though I do believe that such applications will come about naturally as a byproduct of increased understanding of the structure of text.
My current version of the text compression problem has a parsing system built into it. Here is an image showing the output of the parser:
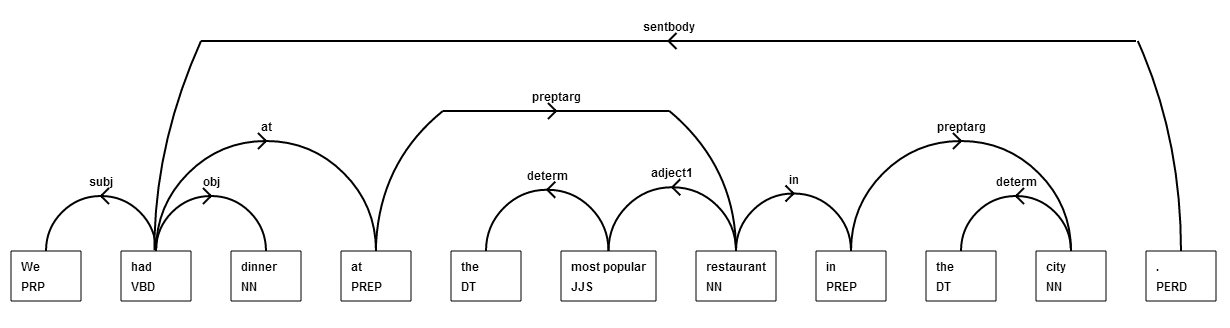
Book
In March of 2011, I completed a solid first draft of my book entitled Notes on a New Philosophy of Empirical Science. This book describes a new approach to empirical science and artificial intelligence. The book can be found online here. At the core of the book is refined version of the scientific method, consisting of the following steps:
- Obtain a large database of measurements relating to a phenomenon of interest.
- Through study of the phenomenon, attempt to develop a theory describing it, or revise a previous theory.
- Instantiate the new theory as a compression program. Invoke the compressor on the database.
- Prefer the new theory to a previous one if it achieves a lower net encoded file size, taking into account the length of the compressor itself.
The key point is that the method can be applied to phenomena that were previously considered outside the scope of traditional empirical science, such as natural images and text corpuses. To compress a dataset requires an understanding of the structure of that dataset, so that for example to achieve a good compression rate for English text requires an understanding of grammatical rules, part-of-speech information, and many other kinds of structure.
The book contains a variety of arguments describing why this method can be expected to lead to new results. The main argument is simply that the theories developed in this way are statements of empirical science analogous to physics. The compression principle provides a clean solution to the Problem of Demarcation, similar but not identical to Popper's principle of falsifiability. The method also explicitly contains a version of Occam's Razor.
Because of the methodological advantages of the method, and because it can be applied to large databases of natural images, the method provides a clean and standard approach to computer vision. In this light, computer vision becomes an empirical science of visual reality. This approach to vision has decisive advantages over the current approach, which is an odd hybrid of mathematics and engineering and suffers from chronic problems in evaluation (how do you evaluate an image segmentation algorithm?) By applying the method to large text databases, one obtains a similarly strong conceptual foundation for the field of computational linguistics. The philosophy of the book also suggests a new approach to the so-called "statistical sciences" such as economics and medicine, which suffer from disastrous methodological shortcomings.
Several papers relating to the ideas presented in the book are available now:
- Daniel Burfoot, "Compression Rate Method for Pure Empirical Science and Application to Computer Vision" arXiv:1005.5181v1
- Daniel Burfoot and Yasuo Kuniyoshi, "Compression Rate Methodology for Pure Empirical Vision Science", Proceedings of the 2009 International Conference on Image Processing, Computer Vision, and Pattern Recognition (IPCV), pp.519--526, 2009. pdf
- Daniel Burfoot, Max Lungarella, and Yasuo Kuniyoshi, "Towards a Theory of Embodied Statistical Learning", Proceedings of the 10th International Conference on the Simulation of Adaptive Behavior (SAB), pp.270--279, 2008. (winner of "Best Philosophy Paper" award) pdf
PhD thesis
The title of my dissertation is "Statistical Modeling as a Search for Randomness Deficiencies", PDF online here. The thesis describes a new principle for statistical modeling, built on the following chain of logic. The Maximum Likelihood principle of traditional statistics is equivalent to a Minimum Codelength principle, due to the codelength-probability equivalence of information theory. So the optimal model for a data set should produce the shortest bit string when used to compress that data set. Now, a bit string cannot be compressed if it is completely random. But if the string is somehow nonrandom, if it contains some structure or pattern, then that structure can be used to reencode the string and achieve a shorter code. This implies that the following strategy can be used to find a good statistical model: encode the dataset as a bit string, then look for randomness deficiencies in the bit string. If one is found, it can be used to update the model and achieve a shorter code.
The main limitation of this idea, and the reason it has not been used extensively in machine learning, is that bit strings are very hard to manipulate. In particular, there is no one-to-one correspondence between bit strings and data samples - some outcomes may require less than a single bit to encode, some may require many bits. The key insight of the thesis is that other representations of the encoded data will work just as well. In particular, one can use the Probability Integral Transform to transform the data from the original space to the [0,1] interval. This produces one PIT value for every data sample. The collection of PIT values can then be searched for randomness deficiencies.
One special type of randomness deficiency occurs when conditioning on a certain outside event. For example, say you have a package of [X,Y] data and you want to predict the Y data from the X data. You transform the Y data into PIT values based on the current model. Then you define a context function F(x) that fires for some x inputs but not others. This implicitly separates the Y data into two subsets. The randomness requirement now says that both subsets must be random: the PIT values must be uniformly distributed on [0,1]. If this is not true, then one can use the context function to update the model. The new model will be better, and the new PIT distribution will be more random.